7
Computer Vision using Convolutional Neural Networks
7.1 Introduction
It
wasn’t
until
recently
computers
were
able
to
reliably
perform
seemingly
easy
tasks
such
as
detecting
a
cat
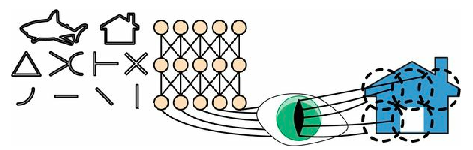
When we look at a picture of a cute puppy, we cannot choose not to see the puppy, not to notice its cuteness. Nor can we explain how we recognize a cute puppy; it’s just obvious to you.
Therefore, we cannot trust our subjective experience.
Perception is NOT a trivial task, and to understand it we must look at how our sensory modules work. CNN s emerged from the study of the brain’s visual cortex, and they have been used in computer image recognition since the 1980s [57]. Over the last 10 years, thanks to the increase in computational power, the amount of available training data, and a much better methods developed for training deep nets, CNN s have managed to achieve impressive performance on some complex visual tasks. Some examples of their application include:
-
Search services: Such as connecting users in the web to the software they need to find [58], [59],
-
Self-driving cars: Such as detecting the colours on a traffic light [60], or detecting the road lines during driving [61],
-
Automatic video classification : i.e., detecting videos and categorising based on content [62],
-
Object Detection: Such as detecting objects in an image [20].
In addition, CNN s are not restricted to visual perception:
They are also successful at many other tasks, such as voice recognition and natural language processing.
However,
as
our
topic
is
Image
Processing
,
we
will
focus
on
its
visual
applications.
In
this
chapter
we
will
explore
where
CNN
s
came
from,
what
their
building
blocks
look
like,
and
how
to
implement
them
using tf.keras.
Then
we
will
discuss
some
of
the
best
CNN
architectures,
as
well
as
other
visual
tasks,
including
object
detection
7.2 Visual Cortex Architecture
In
addition
to
the
previous
revelation
of
how
neurons
work,
they
showed
some
neurons
react
ONLY
to
images
of
horizontal
lines,
while
others
react
ONLY
to
lines
with
different
orientations
-
Fully connected layers,
-
Sigmoid activation functions
5 5 A function allowing non-linear properties for the neural network. ,
but it also introduces two new building blocks:
-
convolutional layers
-
pooling layers.
Which will, of course, will be our focus of attention this chapter.
Information : Limits of DNN
Why not simply use a DNN with fully connected layers for image recognition tasks? Why do we need a new method ?
Unfortunately, although this works fine for small images (e.g., MNIST), it breaks down for larger images due to
the
CNN s solve this problem using partially connected layers and weight sharing.
7.3 Convolutional Layers
The most important building block of a
CNN
is the
Neurons
in
the
first
convolutional
layer
are
NOT
connected
to
every
single
pixel
in
the
input
image
The neurons are only connected to pixels in their
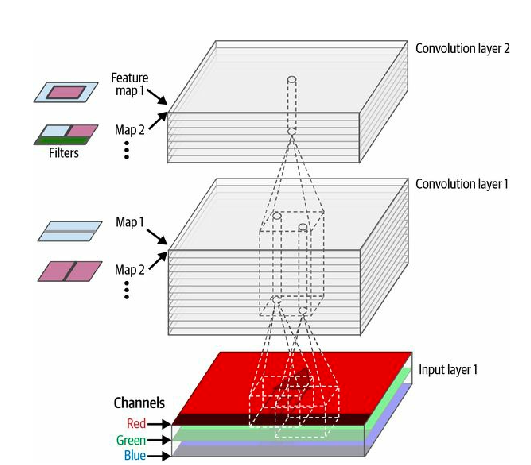
In a CNN , each layer is represented in 2D, which makes it easier to match neurons with their corresponding inputs as our images are also 2D.
In turn, each neuron in the second convolutional layer is connected only to neurons located within a small rectangle in the first layer. This architecture allows the network to concentrate on small low-level features in the first hidden layer, then assemble them into larger higher-level features in the next hidden layer, and so on. This hierarchical structure is common in real-world images, which is one of the reasons why CNN s work so well for image recognition. A neuron located in row , column of a given layer is connected to the outputs of the neurons in the previous layer located in rows to , columns to , where and are the height and width of the receptive field which can be observed in Fig. ??.
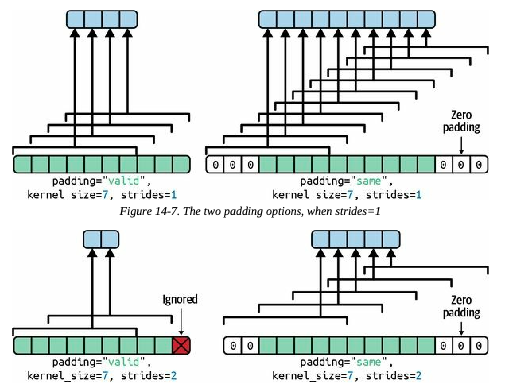
For a layer to have the same height and width as the previous layer, it is common to add zeros around the inputs, which is called
It is also possible to connect a large input layer to a much smaller layer by spacing out the receptive fields, shown in Fig. ??.
This
7.3.1 Filters
A
neuron’s
weights
can
be
represented
as
a
small
image
the
size
of
the
receptive
field.
For
example,
Fig.
7.5
shows
two
The first one is represented as a black square with a vertical white line in the middle.
It’s a 7-by-7 matrix full of 0s except for the central column, which is full of 1s.
Neurons
using
these
weights
will
ignore
everything
in
their
receptive
field
except
for
the
central
vertical
line
We won’t have to define the filters manually: instead, during training the convolutional layer will automatically learn the most useful filters for its task, and the layers above will learn to combine them into more complex patterns.
7.3.2 Stacking Multiple Feature Maps
Up
to
now,
for
simplicity,
We
represented
the
output
of
each
convolutional
layer
as
a
2D
layer,
but
in
reality
a
convolutional
layer
has
multiple
filters
The fact that all neurons in a feature map share the same parameters dramatically reduces the number of parameters in the model. Once the CNN has learned to recognize a pattern in one location, it can recognize it in any other location. In contrast, once a fully connected neural network has learned to recognize a pattern in one location, it can only recognize it in that particular location.
Input images are also composed of multiple sublayers: one per color channel. As we already now, there are typically three: red, green, and blue (RGB). Grayscale images have just one channel, but some images may have many more-for example, satellite images that capture extra light frequencies
Specifically, a neuron located in row , column of the feature map in a given convolutional layer is connected to the outputs of the neurons in the previous layer , located in rows to and columns to ,across all feature maps( in layer ).
Within a layer, all neurons located in the same row i and column j but in different feature maps are connected to the outputs of the exact same neurons in the previous layer.
This definition can be summarised in one big mathematical equation: it shows how to compute the output of a given neuron in a convolutional layer.
Let’s try to understand the variables:
-
is the output of the neuron located in row , column in feature map of the convolutional layer (layer ).
-
are the vertical and horizontal strides, are the height and width of the receptive field, and is the number of feature maps in the previous layer ( ).
-
is the output of the neuron located in layer , row , column , feature map , or channel if the previous layer is the input layer.
-
is the bias term for feature map (in layer ). Think of it as a knob that tweaks the overall brightness of the feature map .
-
is the connection weight between any neuron in feature map of the layer and its input located at row , column (relative to the neuron’s receptive field), and feature map .
7.3.3 Implementing Convolutional Layers with Keras
As with every
ML
application, we load and preprocess a couple of sample images, using sklearn
’s load_sample_image()
function
and Keras’s CenterCrop and Rescaling layers:
Let’s
look
at
the
shape
of
the
images
tensor
It’s
a
4D
tensor.
Let’s
see
why
this
is
a
4D
matrix.
There
are
two
Red, Green, and Blue.
Now let’s create a 2D convolutional layer and feed it these images to see what comes out. For this, Keras provides a
Convolution2D layer, alias Conv2D. Under the hood, this layer relies on TensorFlow’s tf.nn.conv2d()
operation.
Let’s create a convolutional layer with 32 filters, each of size 7-by-7 (using kernel_size=7, which is equivalent to using kernel_size=(7 , 7)
), and apply this layer to our small batch of two
Now let’s look at the output’s shape:
The output shape is similar to the input shape, with two
- 1.
-
There
are
32
channels
instead
of
3.
This
is
because
we
set
filters=32, so we get 32 output feature maps: instead of the intensity of red, green, and blue at each location, we now have the intensity of each feature at each location. - 2.
- The height and width have both shrunk by 6 pixels. This is due to the fact that the Conv2D layer does NOT use any zero-padding by default, which means that we lose a few pixels on the sides of the output feature maps, depending on the size of the filters. In this case, since the kernel size is 7, we lose 6 pixels horizontally and 6 pixels vertically (i.e., 3 pixels on each side).
If instead we set padding="same", then the inputs are padded with enough zeros on all sides to ensure that the output feature
maps end up with the same size as the inputs (hence the name of this option):
These two padding options are illustrated in Fig. 7.8 . For simplicity, only the horizontal dimension is shown here, but of course the same logic applies to the vertical dimension as well.
If the stride is greater than 1 (in any direction), then the output size will not be equal to the input size, even if padding="same".
For example, if we set strides=2
(or equivalently strides=(2, 2)
), then the output feature maps will be 35-by-60: halved both
vertically and horizontally.
Fig. 7.8 shows what happens when strides=2 , with both padding options.
If we are curious, this is how the output size is computed:
-
With
padding="valid", if the width of the input is ih, then the output width is equal to (ih - fh + sh) / sh, rounded down. Recall that fh is the kernel width, and sh is the horizontal stride. Any remainder in the division corresponds to ignored columns on the right side of the input image. The same logic can be used to compute the output height, and any ignored rows at the bottom of the image. -
With
padding="same", the output width is equal to ih / sh, rounded up. To make this possible, the appropriate number of zero columns are padded to the left and right of the input image (an equal number if possible, or just one more on the right side). Assuming the output width is ow, then the number of padded zero columns is (ow - 1) Πsh + fh - ih. Again, the same logic can be used to compute the output height and the number of padded rows.
Now let’s look at the layer’s weights (which were noted wu, v, k’, k and bk in Equation 14-1). Just like a Dense layer, a Conv2D
layer holds all the layer’s weights, including the kernels and biases. The kernels are initialized randomly, while the biases are
initialized to zero. These weights are accessible as TF variables via the weights attribute, or as NumPy arrays via the get_weights()
method:
The kernels array is 4D, and its shape is [ kernel_height, kernel_width, input_channels, output_channels
]. The
biases array is 1D, with shape [ output_channels
]. The number of output channels is equal to the number of output
feature maps, which is also equal to the number of filters. Most importantly, note that the height and width of the
input images do not appear in the kernel’s shape: this is because all the neurons in the output feature maps
share the same weights, as explained earlier. This means that we can feed images of any size to this layer, as
long as they are at least as large as the kernels, and if they have the right number of channels (three in this
case).
Lastly, we will generally want to specify an activation function (such as ReLU) when creating a Conv2D layer, and also specify the corresponding kernel initializer. This is for the same reason as for Dense layers: a convolutional layer performs a linear operation, so if we stacked multiple convolutional layers without any activation functions they would all be equivalent to a single convolutional layer, and they wouldn’t be able to learn anything really complex.
As we can see, convolutional layers have quite a few hyperparameters: filters, kernel_size, padding, strides, activation, kernel_initializer, etc. As always, we can use cross-validation to find the right hyperparameter values, but this is very
time-consuming. We will discuss common
CNN
architectures later in this chapter, to give you some idea of which hyperparameter
values work best in practice.
7.3.4 Memory Requirements
Another challenge with CNN s is that the convolutional layers require a huge amount of RAM. This is especially true during training, because the reverse pass of back-propagation requires all the intermediate values computed during the forward pass.
As
an
example,
consider
a
convolutional
layer
with
200
5-by-5
filters,
with
stride
1
and "same"
padding.
If
the
input
is
a
150-by-100
RGB
image,
then
the
number
of
parameters
is
(5-by-5-by-3+1)
Œ
200
=
15,200
Not as bad as a fully connected layer, but still quite computationally intensive. Moreover, if the feature maps are represented using 32-bit floats, then the convolutional layer’s output will occupy = 96 million bits (12 MB) of RAM. 8 And that’s just for one instance-if a training batch contains 100 instances, then this layer will use up 1.2 GB of RAM.
During inference (i.e., when making a prediction for a new instance) the RAM occupied by one layer can be released as soon as the next layer has been computed, so we only need as much RAM as required by two consecutive layers. But during training everything computed during the forward pass needs to be preserved for the reverse pass, so the amount of RAM needed is (at least) the total amount of RAM required by all layers.
Now
let’s
look
at
the
second
common
building
block
of
CNN
s:
the
7.4 Pooling Layer
The
goal
of
a
pooling
layer
is
to
subsample
(i.e.,
shrink)
the
input
image
to
reduce
the
computational
load,
the
memory
usage,
and
the
number
of
parameters
Just like in convolutional layers, each neuron in a pooling layer is connected to the outputs of a limited number of neurons in the
previous layer, located within a
However, a pooling neuron has NO weights. All it does is aggregate the inputs using an aggregation function such as the max or mean.
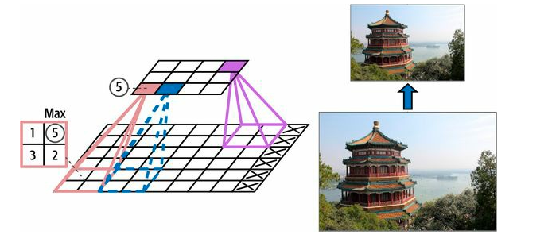
Fig. 7.9 shows a max pooling layer , which is the most common type of pooling layer. In this example, we use a 2-by-2 pooling kernel, with a stride of 2 and no padding. Only the max input value in each receptive field makes it to the next layer, while the other inputs are dropped. For example, in the lower-left receptive field in Fig. 7.9 , the input values are 1, 5, 3, 2, so only the max value, 5, is propagated to the next layer. Because of the stride of 2, the output image has half the height and half the width of the input image (rounded down since we use no padding).
A pooling layer typically works on every input channel independently, so the output depth (i.e., the number of channels) is the same as the input depth.
Other
than
reducing
computations,
memory
usage,
and
the
number
of
parameters,
a
max
pooling
layer
also
introduces
some
level
of
invariance
Here we assume that the bright pixels have a lower value than dark pixels, and we consider three images (A, B, C) going through a max pooling layer with a 2-by-2 kernel and stride 2. Images B and C are the same as image A, but shifted by one and two pixels to the right. As we can see, the outputs of the max pooling layer for images A and B are identical. This is what translation invariance means. For image C, the output is different: it is shifted one pixel to the right (but there is still 50% invariance). By inserting a max pooling layer every few layers in a CNN , it is possible to get some level of translation invariance at a larger scale.
Moreover, max pooling offers a small amount of rotational invariance and a slight scale invariance. Such invariance (even if it is limited) can be useful in cases where the prediction should not depend on these details, such as in classification tasks.
However,
max
pooling
has
some
downsides
too.
It’s
obviously
very
destructive:
even
with
a
tiny
2
Œ
2
kernel
and
a
stride
of
2,
the
output
will
be
two
times
smaller
in
both
directions
(so
its
area
will
be
four
times
smaller),
simply
dropping
75%
of
the
input
values.
And
in
some
applications,
invariance
is
not
desirable.
Take
semantic
segmentation
For this case, if the input image is translated by one pixel to the right, the output should also be translated by one pixel to the right. The goal in this case is equivariance, not invariance: a small change to the inputs should lead to a coresponding small change in the output.
7.5 Implementing Pooling Layers with Keras
The following code creates a MaxPooling2D layer, alias MaxPool2D , using a 2-by-2 kernel. The strides default to the kernel size, so this layer uses a stride of 2 (horizontally and vertically). By default, it uses "valid" padding (i.e., no padding at all):
To create an average pooling layer, just use AveragePooling2D, alias AvgPool2D , instead of MaxPool2D. As we might expect, it works exactly like a max pooling layer, except it computes the mean rather than the max. Average pooling layers used to be very popular, but people mostly use max pooling layers now, as they generally perform better. This may seem surprising, since computing the mean generally loses less information than computing the max. But on the other hand, max pooling preserves only the strongest features, getting rid of all the meaningless ones, so the next layers get a cleaner signal to work with. Moreover, max pooling offers stronger translation invariance than average pooling, and it requires slightly less compute.
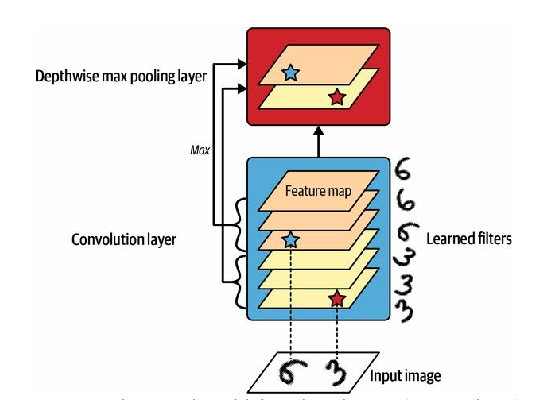
Note that max pooling and average pooling can be performed along the depth dimension instead of the spatial dimensions, although it’s not as common. This can allow the CNN to learn to be invariant to various features. For example, it could learn multiple filters, each detecting a different rotation of the same pattern (such as handwritten digits seen in Fig. 7.11 ), and the depthwise max pooling layer would ensure that the output is the same regardless of the rotation. The CNN could similarly learn to be invariant to anything: thickness, brightness, skew, color, and so on.
Keras does not include a depthwise max pooling layer, but it’s not too difficult to implement a custom layer for that:
class DepthPool(tf.keras.layers.Layer): def__init__ (self, pool_size=2, **kwargs): super().__init__ (**kwargs) self.pool_size = pool_size defcall (self, inputs): shape = tf.shape(inputs)# shape[-1] is the number of channels groups = shape[-1] // self.pool_size# number of channel groups new_shape = tf.concat([shape[:-1], [groups, self.pool_size]], axis=0) return tf.reduce_max(tf.reshape(inputs, new_shape), axis=-1)
This layer reshapes its inputs to split the channels into groups of the desired size (pool_size), then it uses tf.reduce_max()
to
compute the max of each group. This implementation assumes that the stride is equal to the pool size, which is generally what
we want. Alternatively, we could use TensorFlow’s tf.nn.max_pool()
operation, and wrap in a Lambda layer to
use it inside a Keras model, but sadly this op does not implement depthwise pooling for the GPU, only for the
CPU.
One last type of pooling layer that we will often see in modern architectures is the global average pooling layer. It works very differently: all it does is compute the mean of each entire feature map (it’s like an average pooling layer using a pooling kernel with the same spatial dimensions as the inputs). This means that it just outputs a single number per feature map and per instance. Although this is of course extremely destructive (most of the information in the feature map is lost), it can be useful just before the output layer, as we will see later in this chapter. To create such a layer, simply use the GlobalAveragePooling2D class, alias GlobalAvgPool2D:
7.6 CNN Architectures
Typical CNN architectures stack a few convolutional layers (each one generally followed by a ReLU layer), then a pooling layer, then another few convolutional layers (+ReLU), then another pooling layer, and so on. The image gets smaller and smaller as it progresses through the network, but it also typically gets deeper and deeper (i.e., with more feature maps), thanks to the convolutional layers (see Fig. ??). At the top of the stack, a regular feedforward neural network is added, composed of a few fully connected layers (+ReLUs), and the final layer outputs the prediction (e.g., a softmax layer that outputs estimated class probabilities).
A common mistake is to use convolution kernels that are too large. For example, instead of using a convolutional layer with a 5 Π5 kernel, stack two layers with 3 Π3 kernels: it will use fewer parameters and require fewer computations, and it will usually perform better. One exception is for the first convolutional layer: it can typically have a large kernel (e.g., 5 Π5), usually with a stride of 2 or more. This will reduce the spatial dimension of the image without losing too much information, and since the input image only has three channels in general, it will not be too costly.
Here is how we can implement a basic CNN to tackle the Fashion MNIST dataset.
Let’s first download and allocated the traning/testing.
import numpy as np mnist = tf.keras.datasets.fashion_mnist.load_data() (X_train_full, y_train_full), (X_test, y_test) = mnist X_train_full = np.expand_dims(X_train_full, axis=-1).astype(np.float32) / 255 X_test = np.expand_dims(X_test.astype(np.float32), axis=-1) / 255 X_train, X_valid = X_train_full[:-5000], X_train_full[-5000:] y_train, y_valid = y_train_full[:-5000], y_train_full[-5000:]
from functools import partial tf.random.set_seed(42)# extra code ensures reproducibility DefaultConv2D = partial(tf.keras.layers.Conv2D, kernel_size=3, padding="same", activation="relu", kernel_initializer="he_normal") model = tf.keras.Sequential([ DefaultConv2D(filters=64, kernel_size=7, input_shape=[28, 28, 1]), tf.keras.layers.MaxPool2D(), DefaultConv2D(filters=128), DefaultConv2D(filters=128), tf.keras.layers.MaxPool2D(), DefaultConv2D(filters=256), DefaultConv2D(filters=256), tf.keras.layers.MaxPool2D(), tf.keras.layers.Flatten(), tf.keras.layers.Dense(units=128, activation="relu", kernel_initializer="he_normal"), tf.keras.layers.Dropout(0.5), tf.keras.layers.Dense(units=64, activation="relu", kernel_initializer="he_normal"), tf.keras.layers.Dropout(0.5), tf.keras.layers.Dense(units=10, activation="softmax") ])
Let’s go through this code:
- 1.
-
We
use
the
functools.partial()function to define DefaultConv2D, which acts just like Conv2D but with different default arguments: a small kernel size of 3,"same"padding, the ReLU activation function, and its correspondingHe initializer . - 2.
-
We
create
the
Sequential
model.
Its
first
layer
is
a
DefaultConv2D
with
64
fairly
large
filters
(7-by-7).
It
uses
the
default
stride
of
1
because
the
input
images
are
not
very
large.
It
also
sets
input_shape=[28, 28, 1], as the images are 28-by-28 pixels, with a single color channel (i.e., grayscale). - 3.
-
When
we
load
the
Fashion
MNIST
dataset,
we
need
to
make
sure
each
image
has
this
shape.
Therefore
we
may
require
to
use
np.reshape()ornp.expanddims()to add the channels dimension or we could use a Reshape layer as the first layer in the model. - 4.
- We then add a max pooling layer that uses the default pool size of 2, so it divides each spatial dimension by a factor of 2.
- 5.
- We repeat the same structure twice: two convolutional layers followed by a max pooling layer. For larger images, we could repeat this structure several more times. The number of repetitions is a hyperparameter we can tune
-
Observe the number of filters doubles as we climb up the CNN toward the output layer (it is initially 64, then 128, then 256): it makes sense for it to grow, since the number of low-level features is often fairly low (e.g., small circles, horizontal lines), but there are many different ways to combine them into higher-level features. It is a common practice to double the number of filters after each pooling layer: since a pooling layer divides each spatial dimension by a factor of 2, we can afford to double the number of feature maps in the next layer without fear of exploding the number of parameters, memory usage, or computational load.
- 6.
- Next is the fully connected network, composed of two hidden dense layers and a dense output layer. Since it’s a classification task with 10 classes, the output layer has 10 units, and it uses the softmax activation function. Note that we must flatten the inputs just before the first dense layer, since it expects a 1D array of features for each instance. We also add two dropout layers, with a dropout rate of 50% each, to reduce overfitting.
If we compile this model using the "sparse_categorical_crossentropy"
loss and we fit the model to the Fashion MNIST training
set, it should reach over 92% accuracy on the test set.
Over the years, variants of this fundamental architecture have been developed, leading to amazing advances in the field. A good measure of this progress is the error rate in competitions such as the ILSVRC ImageNet challenge. In this competition, the top-five error rate for image classification -that is, the number of test images for which the system’s top five predictions did not include the correct answer-fell from over 26% to less than 2.3% in just six years. The images are fairly large (e.g., 256 pixels high) and there are 1,000 classes, some of which are really subtle (try distinguishing 120 dog breeds).
Looking at the evolution of the winning entries is a good way to understand how CNN s work, and how research in deep learning progresses. We will first look at:
-
LeNet-5 architecture (1998)
-
AlexNet (2012),
-
GoogLeNet (2014),
-
ResNet (2015),
-
SENet (2017).
In addition, we will also briefly look at more architectures, including Xception, ResNeXt, DenseNet, MobileNet, CSPNet, and EfficientNet.
7.6.1 LeNet-5
The LeNet-5 architecture is perhaps the most widely known CNN architecture. As mentioned, it was created by Yann LeCun in 1998 and has been widely used for handwritten digit recognition (MNIST).
| Layer | Type | Maps | Size | Kernel Size |
| Out | Fully Connected | - | 10 | - |
| F6 | Fully connected | - | 84 | - |
| C5 | Convolution | 120 | 1-by-1 | 5-by-5 |
| S4 | Average Pooling | 16 | 5-by-5 | 2-by-2 |
| C3 | Convolution | 16 | 10-by-10 | 5-by-5 |
| S2 | Average Pooling | 6 | 14-by-14 | 2-by-2 |
| C1 | Convolution | 6 | 28-by-28 | 5-by-5 |
| In | Input | 1 | 32-by-32 | - |
As we can see, this looks pretty similar to our Fashion MNIST model: a stack of convolutional layers and pooling layers, followed by a dense network. Perhaps the main difference with more modern classification CNN s is the activation functions: today, we would use ReLU instead of tanh and softmax instead of RBF.
7.6.2 AlexNet
The AlexNet CNN architecture won the 2012 ILSVRC challenge by a large margin: it achieved a top-five error rate of 17%, while the second best competitor achieved only 26%! AlexaNet was developed by Alex Krizhevsky, Ilya Sutskever, and Geoffrey Hinton. It is similar to LeNet-5, only much larger and deeper, and it was the first to stack convolutional layers directly on top of one another, instead of stacking a pooling layer on top of each convolutional layer. Table X presents this architecture.
To reduce overfitting, the authors used two regularization techniques. First, they applied dropout with a 50% dropout rate during training to the outputs of layers F9 and F10. Second, they performed data augmentation by randomly shifting the training images by various offsets, flipping them horizontally, and changing the lighting conditions.
Information : Data Augmentation
It is the process of
The generated instances should be as realistic as possible. This means, in an ideal scenario, a human should not
be able to tell whether it was augmented or not. In adition, it has to be something
For example, we can slightly shift, rotate, and resize every picture in the training set by various amounts and add the resulting pictures to the training set.
To use this feature in code, use Keras’s data augmentation layers, (i.e., RandomCrop, RandomRotation, etc.). These layers
force the model to be more tolerant to variations in the position, orientation, and size of the objects in the pictures. To
produce a model that’s more tolerant of different lighting conditions, we can similarly generate many images with
Data augmentation is also useful when we have an unbalanced dataset: we can use it to generate more samples of the less frequent classes. This is called the synthetic minority oversampling technique (SMOTE).
AlexNet also uses a competitive normalization step immediately after the ReLU step of layers C1 and C3, called
The most strongly activated neurons inhibit other neurons located at the same position in neighboring feature maps.
Such competitive activation has been observed in biological neurons [67]. This encourages different feature maps to specialize, pushing them apart and forcing them to explore a wider range of features, ultimately improving generalization. The following equation gives use a view on how to apply this method:
Let’s discuss what each parameter means:
-
is the neuron’s normalised output located in feature map , at some row and column
17 17 In this equation we consider only neurons located at this row and column, so u and v are not shown . -
is the activation of that neuron
after the ReLU step, butbefore normalisation . -
and are hyperparameters. is called the
bias , and is called thedepth radius . -
is the number of feature maps.
To give an example, if and a neuron has a strong activation , it will inhibit the activation of the neurons located in the feature maps immediately above and below its own.
In AlexNet, the hyperparameters are set as:
We can implement this step by using the tf.nn.local_response_normalization()
function.
A variant of AlexNet called ZF Net was developed by Matthew Zeiler and Rob Fergus and won the 2013 ILSVRC challenge [68]. It is essentially AlexNet with a few tweaked hyperparameters (number of feature maps, kernel size, stride, etc.).
7.6.3 GoogLeNet
The GoogLeNet architecture was developed by Christian Szegedy et al. from Google Research, and won the ILSVRC 2014 challenge by pushing the top-five error rate below 7% [69].
This performance boost came in from the network being
GoogLeNet actually has 10 times fewer parameters than AlexNet
Figure 14-14 shows the architecture of an inception module. The notation
"
" means
the layer uses a 3-by-3 kernel, stride 1, and same
padding. The input signal is first fed to four
Top convolutional layers use different kernel sizes (1-by-1, 3-by-3, and 5-by-5), allowing them to capture patterns at different scales.
Also
note
that
every
single
layer
uses
a
stride
of
1
and
It can be implemented using Keras’s Concatenate
layer, using the default axis=-1.
You may wonder why inception modules have convolutional layers with 1-by-1 kernels.
Surely these layers cannot capture any features because they look at only one pixel at a time, right?
In fact, these layers serve three
- 1.
- Although they cannot capture spatial patterns, they can capture patterns along the depth dimension (i.e., across channels).
- 2.
- They are configured to output fewer feature maps compared to their inputs, so they serve as bottleneck layers , meaning they reduce dimensionality. This cuts the computational cost and the number of parameters, speeding up training and improving generalization.
- 3.
- Each pair of convolutional layers ([1-by-1, 3-by-3] and [1-by-1, 5-by-5]) acts like a single powerful convolutional layer, capable of capturing more complex patterns. A convolutional layer is equivalent to sweeping a dense layer across the image (at each location, it only looks at a small receptive field), and these pairs of convolutional layers are equivalent to sweeping two-layer neural networks across the image.
In short, we can think of the whole inception module as a convolutional layer on steroids, able to output feature maps that capture complex patterns at various scales.
Now let’s look at the architecture of the GoogLeNet
CNN
shown in
Fig.
7.14
. The number of feature maps output by each
convolutional layer and each pooling layer is shown before the kernel size. The architecture is so deep that it has to be
represented in three
All the convolutional layers use the ReLU activation function.
Let’s go through this network together:
-
The first two
(2) layers divide the image’s height and width by 4 (so its area is divided by 16). This reduces the computational load. The first layer uses a large kernel size, 7-by-7, so that much of the information is preserved. -
Then the local response normalization layer ensures that the previous layers learn a wide variety of features .
Information : Local Normalisation Layer
This layer’s job is to create a sort of
-
Two convolutional layers follow, where the first acts like a bottleneck layer. Think of this pair as a single smarter convolutional layer.
-
A local response normalisation layer ensures the previous layers capture a wide variety of patterns.
-
Next, a max pooling layer reduces the image height and width by 2, again to speed up computations.
-
Then comes the CNN ’s backbone: a tall stack of nine
(9) inception modules, interleaved with a couple of max pooling layers to reduce dimensionality and speed up the net. -
Next, the global average pooling layer outputs the mean of each feature map: this drops any remaining spatial information, which is fine because there is not much spatial information left at that point. Indeed, GoogLeNet input images are typically expected to be 224 Π224 pixels, so after 5 max pooling layers, each dividing the height and width by 2, the feature maps are down to 7 Π7.
This classification task, not localization, so it doesn’t matter where the object is.
-
Thanks to the dimensionality reduction brought by the global average pool layer, there is no need to have several fully connected layers at the top of the CNN
20 20 This is unlike AlexNet. , and this considerably reduces the number of parameters in the network and limits the risk of overfitting. -
The last layers are self-explanatory: dropout for regularization, then a fully connected layer with 1,000 units (since there are 1,000 classes) and a softmax activation function to output estimated class probabilities.
The original GoogLeNet architecture included two auxiliary classifiers plugged on top of the third and sixth inception modules. They were both composed:
-
One average pooling layer
-
one convolutional layer
-
two fully connected layers
-
a softmax activation layer
During training, their loss (scaled down by 70%) was added to the overall loss.
The goal adding these auxiliary classifiers was to fight the vanishing gradients problem and regularize the network, but it was later shown that their effect was relatively minor.
Several variants of the GoogLeNet architecture were later proposed by Google researchers, including Inception-v3 [70] and Inception-v4 [71], using slightly different inception modules to reach even better performance.
7.6.4 VGGNet
The runner-up in the ILSVRC 2014 challenge was VGGNet [72], Karen Simonyan and Andrew Zisserman, from the Visual Geometry Group (VGG) research lab at Oxford University, developed a very simple and classical architecture; it had 2 or 3 convolutional layers and a pooling layer, then again 2 or 3 convolutional layers and a pooling layer, and so on, reaching a total of 16 or 19 convolutional layers, depending on the VGG variant. To add to this stack a final dense network with 2 hidden layers and the output layer. It used small 3-by-3 filters, but it had many of them.
7.6.5 ResNet
Kaiming He et al. won the ILSVRC 2015 challenge using a Residual Network (ResNet) that delivered an astounding top-five error rate under 3.6%. The winning variant used an extremely deep CNN composed of 152 layers (other variants had 34, 50, and 101 layers) [73].
Computer vision models are getting deeper and deeper, with fewer and fewer parameters.
The signal feeding into a layer is also added to the output of a layer located higher up the stack.
Let’s see why this is useful. When training a neural network, the goal is simple:
To make it model a target function .
If we add the input to the output of the network (i.e., we add a skip connection), then the network will be forced to model:
This approach is called
When
we
initialise
a
regular
neural
network,
its
weights
are
close
to
zero
If the target function is fairly close to the identity function (which is often the case), this will speed up training considerably.
In addition to the previously mentioned positive aspects, if we add many skip connections, the network can start making progress even if several layers have not started learning yet [74], which we can see the diagram in Fig. 7.15 .
Skip connections allows the signal to easily make its way across the whole network.
The deep residual network can be seen as a stack of residual units (RUs), where each residual unit is a small neural network with a skip connection. Now let’s look at ResNet’s architecture (see Figure 14-18).
The idea of ResNet is simple to describe. It starts and ends exactly like GoogLeNet (except without a dropout layer), and in between
is just a very deep stack of residual units. Each residual unit is composed of two "same"
padding).
The number of feature maps is doubled every few residual units, at the same time as their height and width are halved (using a convolutional layer with stride 2)
There are different variations of this aforementioned architecture, each having different numbers of layers. ResNet-34, as the name implies, is a ResNet with 34 layers (only counting the convolutional layers and the fully connected layer) containing 3 RUs that output 64 feature maps, 4 RUs with 128 maps, 6 RUs with 256 maps, and 3 RUs with 512 maps.
ResNets deeper than that, such as ResNet-152, use slightly different residual units. Instead of two
- 1.
- a 1-by-1 convolutional layer with just 64 feature maps (4x less), which acts as a bottleneck layer (as discussed already)
- 2.
- a 3-by-3 layer with 64 feature maps
- 3.
- another 1-by-1 convolutional layer with 256 feature maps (4 times 64) that restores the original depth
ResNet-152 contains 3 such RUs that output 256 maps, then 8 RUs with 512 maps, a whopping 36 RUs with 1,024 maps, and finally 3 RUs with 2,048 maps.
7.7 Implementing a ResNet-34 CNN using Keras
Most
CNN
architectures
described
so
far
can
be
implemented
easily
using
Keras
First,
we’ll
create
a ResidualUnit
layer:
DefaultConv2D = partial(tf.keras.layers.Conv2D, kernel_size=3, strides=1, padding="same", kernel_initializer="he_normal", use_bias=False) class ResidualUnit(tf.keras.layers.Layer): def__init__ (self, filters, strides=1, activation="relu", **kwargs): super().__init__ (**kwargs) self.activation = tf.keras.activations.get(activation) self.main_layers = [ DefaultConv2D(filters, strides=strides), tf.keras.layers.BatchNormalization(), self.activation, DefaultConv2D(filters), tf.keras.layers.BatchNormalization() ] self.skip_layers = [] if strides > 1: self.skip_layers = [ DefaultConv2D(filters, kernel_size=1, strides=strides), tf.keras.layers.BatchNormalization() ] defcall (self, inputs): Z = inputs for layer in self.main_layers: Z = layer(Z) skip_Z = inputs for layer in self.skip_layers: skip_Z = layer(skip_Z) return self.activation(Z + skip_Z)
As we can see, this code matches Figure 14-19 pretty closely. In the constructor, we create all the layers we will need:
the
main
layers
are
the
ones
on
the
right
side
of
the
diagram,
and
the
skip
layers
are
the
ones
on
the
left
Then in the call()
method, we make the inputs go through the main layers and the skip layers (
Now we can build a ResNet-34 using a
ResidualUnit
class.
The code closely matches:
model = tf.keras.Sequential([ DefaultConv2D(64, kernel_size=7, strides=2, input_shape=[224, 224, 3]), tf.keras.layers.BatchNormalization(), tf.keras.layers.Activation("relu"), tf.keras.layers.MaxPool2D(pool_size=3, strides=2, padding="same"), ]) prev_filters = 64 for filters in [64] * 3 + [128] * 4 + [256] * 6 + [512] * 3: strides = 1 if filters == prev_filters else 2 model.add(ResidualUnit(filters, strides=strides)) prev_filters = filters model.add(tf.keras.layers.GlobalAvgPool2D()) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(10, activation="softmax"))
The only tricky part in this code is the loop that adds the ResidualUnit
layers to the model. As explained earlier:
-
the first 3 RUs have 64 filters,
-
the next 4 RUs have 128 filters.
and so on. At each iteration, we must set the stride to 1 when the number of filters is the same as in the previous RU, or else we
set it to 2; then we add the ResidualUnit, and finally we update prev_filters.
With just 40 lines of code, we can build the model that won the ILSVRC 2015 challenge. This demonstrates both the elegance of the ResNet model and the expressiveness of the Keras API. Implementing the other CNN architectures is a bit longer, but not much harder.
However, Keras comes with several of these architectures built in, so why not use them instead?
7.8 Using Pre-Trained Models from Keras
In general, we don’t have to implement standard models like GoogLeNet or ResNet manually, as pre-trained networks are readily
available using the tf.keras.applications
package.
For example, we can load the ResNet-50 model, pre-trained on ImageNet, with the following line of code:
This was surprisingly simple. This will create a ResNet-50 model and download weights already trained
on the ImageNet dataset. To use it, we first need to ensure the images have the correct size. A
ResNet-50 model expects an image with the dimensions of 224-by-224-pixel
The pre-trained models assumes the images are
preprocess_input()
function we can use to
pre-process our images. These functions assume the original pixel values range from 0 to 255, which is the case
here:
Now we can use the pre-trained model to make predictions:
As usual, the output
Y_proba
is a matrix with
decode_predictions()
function. For each image, it returns an array containing the top
K
predictions, where each prediction is represented as an array containing the class identifier, its name, and the corresponding
confidence score:
The output looks like this:
The correct classes are palace and dahlia (which you can see in Fig. 7.18 ), so the model is correct for the first image but wrong for the second .
This is caused by dahlia not being part of the 1,000 ImageNet classes.
Many
vision
models
are
available
in tf.keras.applications,
from
lightweight
and
fast
models
to
large
and
accurate
ones.
But
what
if
we
want
to
use
an
image
classifier
for
classes
of
images
that
are
not
part
of
ImageNet?
In
that
case,
we
may
still
benefit
from
the
pre-trained
models
by
using
them
to
perform
transfer
learning
.
7.9 Pre-Trained Models for Transfer Learning
If we want to build an
First, we’ll load the flowers dataset using TensorFlow Datasets:
We can get information about the dataset by setting with_info=True.
"train"
dataset, no test set or validation set, so we need to split the training set. Let’s call
tfds.load()
again, but this time taking the first 10% of the dataset for testing, the next 15% for validation, and the remaining
75% for training:
All three
We need to batch them, but first we need to ensure they all have the same size, otherwise batching will fail. We can use a Resizing
layer for this. We must also call the tf.keras.applications. xception.preprocess_input()
function to
preprocess the images appropriately for the Xception model. Lastly, we’ll also shuffle the training set and use
prefetching:
batch_size = 32 preprocess = tf.keras.Sequential([ tf.keras.layers.Resizing(height=224, width=224, crop_to_aspect_ratio=True), tf.keras.layers.Lambda(tf.keras.applications.xception.preprocess_input) ]) train_set = train_set_raw.map(lambda X, y: (preprocess(X), y)) train_set = train_set.shuffle(1000, seed=42).batch(batch_size).prefetch(1) valid_set = valid_set_raw.map(lambda X, y: (preprocess(X), y)).batch(batch_size) test_set = test_set_raw.map(lambda X, y: (preprocess(X), y)).batch(batch_size)
Now each batch contains 32 images, all of them 224-by-224 pixels, with pixel values ranging from -1 to 1.
This is the ideal values for training such a network. As the dataset is not very large, a bit of data augmentation will certainly help. Let’s create a data augmentation model that we will embed in our final model. During training, it will randomly flip the images horizontally, rotate them a little bit, and tweak the contrast:
Next let’s load an Xception model, which is pre-trained on ImageNet. We exclude the top of the network by setting include_top=False. This excludes the global average pooling layer and the dense output layer. We then add our own global
average pooling layer (feeding it the output of the base model), followed by a dense output layer with one unit per class, using
the softmax activation function. Finally, we wrap all this in a Keras Model:
tf.random.set_seed(42)# extra code ensures reproducibility base_model = tf.keras.applications.xception.Xception(weights="imagenet", include_top=False) avg = tf.keras.layers.GlobalAveragePooling2D()(base_model.output) output = tf.keras.layers.Dense(n_classes, activation="softmax")(avg) model = tf.keras.Model(inputs=base_model.input, outputs=output)
It’s usually a good idea to freeze the weights of the pre-trained layers, at least at the beginning of training
Finally, we can compile the model and start training:
After training the model for a few epochs, its validation accuracy should reach a bit over 80% and then stop improving. This means that the top layers are now pretty well trained, and we are ready to unfreeze some of the base model’s top layers, then continue training.
For example, let’s unfreeze layers 56 and above (that’s the start of residual unit 7 out of 14, as you can see if you list the layer names):
Don’t forget to compile the model whenever you freeze or unfreeze layers. Also make sure to use a much lower learning rate to avoid damaging the pre-trained weights:
This model should reach around 92% accuracy on the test set, in just a few minutes of training (with a GPU). If you tune the hyperparameters, lower the learning rate, and train for quite a bit longer, you should be able to reach 95% to 97%.
But there’s more to computer vision than just classification. For example, what if you also want to know where the flower is in a picture? Let’s look at this now.
tf.random.set_seed(42)# extra code ensures reproducibility base_model = tf.keras.applications.xception.Xception(weights="imagenet", include_top=False) avg = tf.keras.layers.GlobalAveragePooling2D()(base_model.output) class_output = tf.keras.layers.Dense(n_classes, activation="softmax")(avg) loc_output = tf.keras.layers.Dense(4)(avg) model = tf.keras.Model(inputs=base_model.input, outputs=[class_output, loc_output]) optimizer = tf.keras.optimizers.SGD(learning_rate=0.01, momentum=0.9)# added this line model.compile(loss=["sparse_categorical_crossentropy", "mse"], loss_weights=[0.8, 0.2],# depends on what you care most about optimizer=optimizer, metrics=["accuracy", "mse"])